|
|
Noticia: Momento de inercia y resistencia a la rodadura
|
|
|

2) MOMENTO DE INERCIA Y RESISTENCIA A LA RODADURA
- Momento de inercia
- Resistencia a la rodadura
- Elección de compuestos, perfiles, anchuras, secciones, dibujos y diámetros.
La
Ley de la Conservación de la Energía nos indica que la energía
potencial que tenemos en la salida 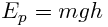 Ep: Energía potencial en
Julios, m:masa en Kg, g:aceleración de la gravedad=9,8m/s2, h:altura en
metros, se transformará en un punto de la rampa en Energía cinética Ep: Energía potencial en
Julios, m:masa en Kg, g:aceleración de la gravedad=9,8m/s2, h:altura en
metros, se transformará en un punto de la rampa en Energía cinética 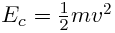 Ec: Energía cinética en Julios m: masa en Kg, v:velocidad
en m/s. Ec: Energía cinética en Julios m: masa en Kg, v:velocidad
en m/s.
En la práctica, esta energía potencial se "desperdicia"
en unos cuantos componentes más, cuando solo nos interesa la energía
cinética, que es la única que se transforma en velocidad. Ep = Ec + Ec
angular de las ruedas + resistencia a la rodadura + rozamiento
aerodinámico + rozamiento mecánico
El momento de inercia y la resistencia a la rodadura son dos de los aspectos de la dinámica que más se prestan a los "mitos" y a las ideas preconcebidas. Vamos a tratar de aclararlo un poco...
Momento de inercia ( moment of inertia )
Cuando estudiamos movimientos circulares, como el de la rueda tenemos que "traducir" todas las ecuaciones lineares en angulares.
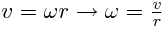
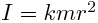
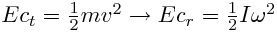
La velocidad lineal de la goitibera se traduce en una velocidad angular de las ruedas al girar. Cuanto mayor sea la velocidad o menor el radio de la rueda, más rápido girará esta.
La Ec de las ruedas tiene dos componentes, una lineal debido a su traslación que funcioina igual que la masa del chasis 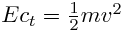 más otra rotacinoal debido al giro alrededor de su eje más otra rotacinoal debido al giro alrededor de su eje 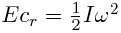 . Esta segunda Ec no se traduce en velocidad lineal y causa que una rueda descienda más rápido una pendiente deslizando ( si su rozamiento fuese igual a cero ) que girando. La goitibera va "tirando" de las ruedas, que aun girando libremente, le van frenando ligeramente. . Esta segunda Ec no se traduce en velocidad lineal y causa que una rueda descienda más rápido una pendiente deslizando ( si su rozamiento fuese igual a cero ) que girando. La goitibera va "tirando" de las ruedas, que aun girando libremente, le van frenando ligeramente.
En algunos casos, como en el volante de inercia de un motor o de un juguete, esta energía se puede aprovechar acumulándola cuando nos interesa ( en la bajada del pistón de un motor, en la frenada de un KERS ( aunque el mecanismo sea eléctrico, el fundamento es el mismo ) y recuperándola cuando queremos ( en el punto muerto de un pistón o en la recta descargando el KERS ). En nuestro caso, como las ruedas no son desembragables, acumulan energía continuamente ( y no cuando nosotros queremos, como en una frenada ). Además esta energía se pierde irremediablemente cada vez que frenamos y solo es útil en los llanos o ligeras subidas tras una recta con fuerte bajada en la que pueden ayudar a vencer la resistencia aerodinámica de ese tramo. Por esto ( y por otros motivos que veremos más adelante ) nos interesa tener unas ruedas ligeras ( o, mejor dicho, con un bajo momento de inercia ).
El momento de inercia es el equivalente a la masa en las ecuaciones de dinámica angular. Simplemente es la suma de la masa de cada partícula de la rueda por su distancia al eje ( su radio ). Es intuitivo que nos cuesta más girar una rueda cuanto más peso tiene y cuanto más lejos se halla éste del eje. La suma de infinitas partículas infinitesimales se resuleve mediante una integración, y la fórmula final para el momento de inercia es:
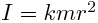
Donde I: momento de inercia en Kg.m2, m:masa en Kg, r: radio en m y k es una constante que indica el ratio de distribución de la masa a lo largo de la rueda. Para un disco sólido ( la masa uniformemente repartida entre el eje y el radio exterior ) K=0,5 y para un anillo ( toda la masa en el radio exterior ) K=1. En la práctica, para una rueda con llanta solida k puede oscilar aproximadamente entre 0,6 si la cubierta es muy ligera ( como una 12/12 x 2 1/4 en una llanta de magnesio de 8" ) y 0,8-0,9 si la cubierta es muy pesada ( como una 16x4 en la misma llanta ).
Puedes calcular el momento de inercia matemáticamente suponiendo un valor de K, sumando los momentos de inercia de cada componente ( descomponiéndolo en elementos básicos como discos, anillos o toros ) o calcularlo experimentalmente como veremos en un futuro artículo. Te adelantamos que el momento de inercia de la rueda con el neumático de 16x4 es más de 4 veces superior al de la rueda con el neumático 12 1/2 x 2 1/4.
Resumiendo, que para tener unas ruedas con un bajo momento de inercia debenos de reducir el peso en la parte más alejada del eje ( es mucho más importante el neumático que la lllanta ). En este clásico experimento se comprueba que, entre dos ruedas de
idéntico peso, desciende más rápido la que tiene menor momento de
inercia ( en este caso, la que tiene los lastres más cerca del eje ).

De todas maneras, tampoco te vuelvas loco: considera que el peso total de las 4 ruedas no suele llegar a los 10 Kg contra los 200 Kg totales. Si te molestas en calcular la pérdida de velocidad de las ruedas 16x4 debido al incremento de su Ec rotacional comprobarás que es algo menor a 1 Km/h a una velocidad de 72 Km/h. Hay que tenerlo en cuenta pero la resistencia a la rodadura, la resistencia aerodinámica, el agarre y la capacidad de frenada son variables tan importante o más que el momento de inercia.
Resumiendo, en el momento de inercia de una rueda ( y consiguientemente en su capacidad de aceleración y en la velocidad final que alcanza ):
- NO INFLUYEN: El peso total de la rueda ni el diámetro de la misma.
- SÍ INFLUYE: La distribución de la masa de la misma, siendo más rápidas las ruedas con más masa cerca del eje y menos masa lejos de él. Es inútil gastar dinero en una llanta ligera y mantener un neumático pesado.
Vídeo comparativo.
Tienes más información sobre la influencia del momento de inercia de las ruedas en la velocidad en la comparativa de ruedas de carrilana.
Resistencia a la rodadura ( rolling resistance )
El mecanismo de compresión y expansión del neumático que hemos visto en el apartado de agarre genera una fuerza que se opone al giro de la rueda y que se localiza ligeramente por delante del centro de la huella. Es importante comprender que NO ES UN ROZAMIENTO, ES UNA FUERZA.
Para disminuirla deberemos disminuir la cantidad de deformación de la huella, la energía disipada en la compresión-expansión o la distancia entre el punto de aplicación de la fuerza y el centro de la huella:
- Velocidad: La resistencia a la rodadura ( RR ) aumenta ligeramente con la velocidad ya que aumentan las vibraciones del neumático con el asfalto lo que incrementa ligeramente la intensidad del ciclo de compresión-expansión. Un aumento de 40 Km/h a 80 Km/h incrementa aproximadamente un 3% la RR.
- Carga soportado: A mayor carga soportada ( peso más carga aerodinámica ) mayor resistencia a la rodadura ya que se produce mayor deformación del neumático. Este efecto - y el del aumento de velocidad - se ven compensados, solo parcialmente, por el aumento de temperatura producido al aumentar la intensidad del ciclo de compresión-expansión. Esta temperatura de equilibrio más elevada se alcanza en los vehículos de turismo al cabo de varios minutos.
- Temperatura: El aumento de temperatura tiene dos efectos. Por un lado disminuye el grado de histéresis de la goma por lo que se pierde menos energía en el ciclo de compresión-expansión. Adicionalmente hace que aumente la presión del aire contenido en la rueda, disminuyendo de nuevo la resistencia a la rodadura. Un amumento de 1ºC representa entre u 0,5% y 1% de disminución en la resistencia a la rodadura.
- Lluvia: Cuando el asfalto está mojado, la resistencia a la rodadura aumenta aproximadamente en un 10% por la bajada de temperatura y por la energía perdida en el desplazamiento del agua bajo la huella.
- Construcción de la rueda: Un neumático radial tiene una banda de rodadura más rígida y unos flancos más flexibles. Un neumático diagonal ( bias type ) tiene una banda de rodadura más flexible y unos flancos más rígidos. Dado que la gran mayoría de las pérdidas por histéresis de la rueda se producen en la banda de rodadura, a igualdad de características, un neumático radial tiene un 30% menos de resistencia a la rodadura que uno diagonal.
- Presión de inflado: Una mayor presión hace que la huella se deforme menos bajo la misma carga. Dentro de los límites de presión soportables por un neumático la RR disminuye con los aumentos de presión de inflado. Por eso es habitual utilizar la presión máxima admitida por el neumático o por el reglamento de la categoría. En utilización fuera de carretera esto no simpre es así ya que el efecto negativo del rebote contra los obstáculos puede sobrepasar esta disminución. Pero con el grado de uniformidad que tienen la mayoría de carreteras, a mayor presión menor RR.
- Índice de carga: Un neumático diseñado para soportar más carga puede tener más lonas en su carcasa lo que incrementa ligeramente el rozamiento entre las mismas y con ello la energía perdida. En los neumáticos diagonales, un incremento de 3 a 6 en el número de lonas incrementa la resistencia a la rodadura en un 5%. Como contrapartida, los neumáticos con un índice de carga mayor suelen tener presiones de inflado máximo más altas, por lo que pueden compensar con creces este efecto.
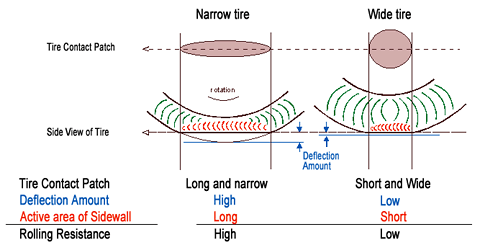
- Dibujo: Todo dibujo en la banda de rodadura aumenta la resistencia a la rodadura. Tomando como base un neumático totalmente liso, si aumentamos el dibujo de manera que solo el 60 de la banda de rodadura contacte con el asfalto y que el 40% restante sean canales y surcos, la RR aumentará UN 25%. Esto es debido a que los canales permiten que la goma se desplace de su posición de reposo con más facilidad, lo que incrementa las pérdidas de energía en la banda de rodadura.
- Composición de la goma: Influye directamente en el grado de histéresis. A mayor "rebote" de la misma, menor pérdida de energía y menor RR. Desgraciadamente, esto suele conllevar un menor coeficiente de rozamiento y, por ello, un menor agarre.
- Hilos de la carcasa: Su influencia es muy reducida, del orden del 6% de la RR de la carcasa. Unos hilos más finos pierden menos energía por frotamiento. Sin embargo, su mayor papel es el de reducir las deformaciones de la goma a la que están adheridos.
- Perfil de la rueda: Un perfil más bajo ( menor altura de los flancos ) ofrece menor RR ya que permite una menor flexión de los mismos con menos pérdidas de energía.
- Rugosidad del asfalto: Tomando como base el cemento pulido, el asfalto gastado aumenta la RR en un 1% y el asflato nuevo y abrasivo en un 8%.
- Radio de la rueda: Un radio mayor se ve menos afectado por las irregularidades del terreno. Una rueda más pequeña "se cae más profundo" en las irregularidades. Si el resto de características son iguales, una rueda de mayor radio tiene menor resistencia a la rodadura. Sin embargo, una rueda de mayor diámetro suele implicar una mayor resstencia aerodinámica que puede contrarestar este efecto.
Elección de diámetros, perfiles y compuestos.
- Elección de compuestos: una goma más blanda tendrá mejor agarre en curva ( si trabaja en el rango de temperaturas para el que está diseñada, por eso las ruedas de competición de rallie, moto de circuito, etc. no funcionan en goitibera, porque necesitan temperaturas cercanas a los 100ºC ). Sin embrago, su resistencia a la rodadura aumentará. Lo ideal sería poder elegir entre varias durezas en función del número y la dificultad de las curvas de la bajada, con gomas más blandas para circuitos muy técnicos y gomas más duras para circuitos con largas rectas.
- Elección de perfil: Un perfil más bajo nos ayuda a disminuir la resistencia a la rodadura y la flexión de los flancos ante cargas laterales, por lo que debería de aumentar la capacidad de agarre lateral del neumático.
Hay que tener en cuenta que el peso total de una goitibera ( por ejemplo 200 Kg de una Cx ) unido a la alta presión de las ruedas ( 4,9 bar de máximo autorizaso ), hace que esta flexión lateral sea muy reducida, por lo que la ganancia de agarre lateral puede ser más teórica que práctica. A esto hay que unir que generalmente la llanta pesa más que el neumático, por lo que debemos de tener cuidado de no aumentar el momento de Inercia de la rueda al colocar una llanta de más diámetro y un neumático de perfil más bajo por la pérdida de Energía cinética que supone, además de sus efectos negativos en suspensiones y frenos.
- Elección de anchura y sección: Ya hemos visto que una huella más ancha disminuye la resistencia ala rodadura y aumenta la capacidad de agarre lateral. Sin embargo, suele implicar un mayor peso del neumático, un mayor momento de inercia y una mayor resistencia aerodinámica. La sección redondeada ( tipo moto ) es muy habitual porque los neumáticos diagonales tienen, por construcción, una forma redondeada, y cualquier sección más cuadrada se logra a base de añadir goma en los flancos, con el aumento de peso que representa.
Por ello es habitual usar ruedas de perfil redondeado a las que se desgasta la banda de rodadura hasta lograr una huella plana de unos 3-5 cm de anchura.
- Elección de dibujo: Lo más eficiente, en términos de agarre y resistencia a la rodadura y agarre es el dibujo completamente liso. Solo tendría sentido de utilizar dibujo en condiciones de lluvia ( que estudiaremos en el capítulo 12 )
- Elección de diámetro: un diámetro mayor nos otorga una resistencia a la rodadura menor. Sin embargo suele implicar un mayor momento de inercia. Pero esto no influye en la Ecr:
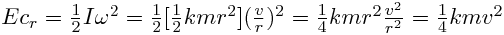
Es decir, que aunque una rueda de mayor diámeto tiene un mayor momento de inercia, su velocidad angular es menor ( gira menos veces por minuto ). La Ecr es independiente del radio de la rueda. Por ello, parece razonable acercarse al diámetro de rueda máximo permitido por el reglamento ( siempre que la resistencia aerodinámica no aumente demasiado ) pero cuidando la distribución de la masa dentro de la misma ( disminuyendo k a base de aligerar las partes de la rueda más alejadas del eje: básicamente el neumático ).
Si tuviésemos dos ruedas idénticas en un laboratorio ( imagina dos cilindros de madera ) en los que la única diferencia fuese el diámetro, las dos descenderían a la misma velocidad. El cilindro grande tendría mayor momento de inercia pero menor velocidad angular.
Ahora te animo a que eches un vistazo a este interesante vídeo: una carrera en laboratorio entre distintos tipos de "ruedas". ¿ Adivinarás quién ganará cada carrera antes de la salida ?
|
| |
Puntuación Promedio: 4.28
votos: 7

|
|











